Analisis Algoritma

Algoritma Greedy

Algoritma Greedy merupakan metode yang paling populer untuk memecahkan persoalan optimasi.

Persoalan optimasi (optimization problems), persoalan mencari solusi optimum. Algoritma greedy membentuk solusi langkah per langkah (step by step). Prinsip utama algoritma greedy adalah ?take what you can get now!?. Maksud dari prinsip tersebut adalah pada setiap langkah dalam algoritma greedy, kita ambil keputusan yang paling optimal untuk langkah tersebut tanpa memperhatikan konsekuensi pada langkah selanjutnya. Kita namakan solusi tersebut dengan optimum lokal. Kemudian saat pengambilan nilai optimum lokal pada setiap langkah, diharapkan tercapai optimum global, yaitu tercapainya solusi optimum yang melibatkan keseluruhan langkah dari awal sampai akhir.

Elemen-elemen algoritma greedy:

1. Himpunan kandidat, C.

2. Himpunan solusi, S

3. Fungsi seleksi (selection function)

4. Fungsi kelayakan (feasible)

5. Fungsi obyektif

Dengan kata lain:

algoritma greedy melibatkan pencarian sebuah himpunan bagian, S, dari himpunan kandidat, C; yang dalam hal ini, S harus memenuhi beberapa kriteria yang ditentukan, yaitu menyatakan suatu solusi dan S dioptimisasi oleh fungsi obyektif.

Contoh Kasus :

1. Penerapan Greedy di dalam Penukaran Uang

- Koin: 5, 4, 3, dan 1

Uang yang ditukar = 7.

Solusi greedy: 7 = 5 + 1 + 1 ( 3 koin) --> tidak optimal

Solusi optimal: 7 = 4 + 3 ( 2 koin)

- Koin: 10, 7, 1

Uang yang ditukar: 15

Solusi greedy: 15 = 10 + 1 + 1 + 1 + 1 + 1 (6 koin)

Solusi optimal: 15 = 7 + 7 + 1 (hanya 3 koin)

- Koin: 15, 10, dan 1

Uang yang ditukar: 20

Solusi greedy: 20 = 15 + 1 + 1 + 1 + 1 + 1 (6 koin)

Solusi optimal: 20 = 10 + 10 (2 koin)

Penyelesaian dengan exhaustive search

- Terdapat 2ⁿ kemungkinan solusi

(nilai-nilai X = {x₁, x₂, …, x_n} )

- Untuk mengevaluasi fungsi obyektif = O(n)

- Kompleksitas algoritma exhaustive search seluruhnya = O(n × 2ⁿ ).

Penyelesaian dengan algoritma greedy
Strategi greedy : Pada setiap langkah, pilih koin dengan nilai terbesar dari himpunan koin yang tersisa.

2. Penerapan Greedy di dalam Transportasi (Knapsack Problem)

Pada tabel 1 terdapat sebuah alat angkut dengan dengan kapasitas 100 kg terdapat 4 buah barang dengan ukuran sebagai berikut :

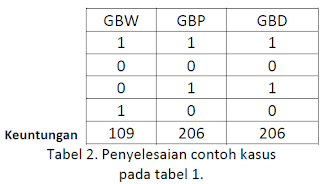
Maka dengan menggunakan algoritma Greedy diperoleh Tabel 2 sebagai berikut :

Keterangan :

GBW : Greedy By Weight

GBP : Greedy By Profit

GBD : Greedy By Density

0 : Barang tidak diangkut

1 : Barang diangkut

pseudocode algoritma greedy Knapsack Problem adalah sebagai berikut :

function Knapsack(input C : himpunan_objek, K : real) --> himpunan_solusi

{ Menghasilkan solusi persoalan knapsack dengan algoritma greedy yang

menggunakan strategi pemilihan objek berdasarkan profit(pi),weight(wi),

density (pi/wi). Solusi dinyatakan sebagai vektor X = x[1], x[2], …,

x[n]. Asumsi: Untuk Greedy by profit seluruh objek sudah terurut

berdasarkan nilai pi yang menurun. Untuk Greedy by weighted seluruh objek

sudah terurut berdasarkan nilai wi yang menaik. Untuk Greedy by density

seluruh objek sudah terurut berdasarkan nilai pi/wi yang menurun.}

Deklarasi

i, TotalBobot : integer

Avalaible : boolean

x : himpunan_solusi

Algoritma

for i <--1 to n do

x[i] <-- 0 { inisialisasi setiap status pengambilan objek i dengan 0 }

endfor

i <-- 0

TotalBobot <-- 0

Available <-- true

while (i ≤ n) and (Available) do

{ cek objek ke-i }

i <-- i + 1

if ( TotalBobot + w[i] ≤ K )

then

{ masukkan objek Ci ke dalam knapsack }

x[i] <-- 1

TotalBobot <-- TotalBobot + w[i]

else

Available <-- false

x[i] <-- 0

{ objek Ci tidak dimasukkan ke dalam knapsack }

endif

endwhile

{ i > n or not Available }

return x

endfunction

3. Penerapan Greedy dalam Permainan Monopoli

- Analisis Masalah

Monopoli memuat beberapa petak-petak yang memiliki harga dan sewa tertentu. Pemain monopoli diberikan sejumlah uang untuk dapat membeli petak-petak tersebut sehingga mampu menjadi paling kaya dan paling banyak menguasai petak. Permasalahan utama dari permainan monopoli ini adalah bagaimana seorang pemain mampu mengoptimalkan uang yang dimilikinya sehingga mampu memperoleh petak- petak yang potensial. Pada akhirnya, pemain mampu mencapai tingkat kekayaan tertinggi dengan memanfaatkan kesempatan seminimal mungkin.

Frekuensi penempatan tiap petak oleh bidak pemain monopoli juga dihitung.

Berikut ini adalah tabel frekuensi per 10 putaran yang kami analisis berdasarkan simulasi permainan.

- Contoh Kasus

Misalkan seorang pemain yang baru memulai permainan memperoleh modal sejumlah M rupiah. Dan disediakan petak-petak daerah sebanyak N-buah dalam permainan untuk dibeli oleh pemain. Setiap petak memiliki properti (cost) ci dan keuntungan (profit) pi . Objektif persoalan adalah memilih petak-petak yang akan dibeli sedemikian sehingga memaksimumkan keutungan.

Permasalahan dari permainan monopoli ini berdasarkan algoritma Greedy dapat didekati melalui tiga solusi :

1. Greedy by density menyelesaikan permasalahan dengan melihat perbandingan antara harga dan keuntungan yang didapat. Penyelesaian ini juga melibatkan aspek frekuensi suatu petak dikunjungi.

2. Greedy by profit , pemecahan masalah dilakukan dengan melihat keuntungan yang dapat

diraih dari tiap petak. Pemecahan ini juga melibatkan aspek frekuensi dalam menentukan

petak-petak monopoli yang potensial.

3. Greedy by cost mendekati permasalahan dengan melihat perbandingan harga antar petak pada monopoli. Harapan dari solusi ini adalah memperoleh jumlah petak sebanyak-banyaknya.

pseudocode algoritma greedy untuk pemilihan petak adalah sebagai berikut :

procedure UrutByDensity (input/output C : himpunan_petak)

{Mengurutkan petak-petak berdasarkan density (profit*frequency/cost)}

procedure UrutByProfit(input/output C : himpunan_petak)

{Mengurutkan petak-petak berdasarkan profit tiap petak}

procedure UrutByCost(input/output C : himpunan_petak)

{ Mengurutkan petak-petak berdasarkan cost tiap petak}

function CariProfitMaks (M : integer, C : himpunan_petak, mtd : string) --> himpunan_petak

{ Mengembalikan himpunan_petak yang terpilih dengan modal M, domain himpunan_petak C, dan mtd metode pencarian yang dipilih }

Deklarasi

Cost,i,j : integer

H : himpunan_petak

Algoritma

if (mtd = ‘density’) then

SortByDensity(C)

else if (mtd = ‘profit’) then

SortByProfit(C)

else

SortByCost(C)

endif

Cost <-- 0

i <-- 0

j <-- 0

while ((Cost < M) and (i < 22))

if (Cost+C[i].GetCost() < M)

then

Cost <-- Cost+C[i].GetCost()

H[j] <-- C[i]

j++

endif

i++

endwhile

return H

endfunction

4. Penerapan Greedy dalam Permainan Bantumi

- Bentuk representasi permainan bantumi dalam bahasa pemrograman:

1. ArrayP adalah larik yang berisi jumlah batu yang terdapat pada lubang di sisi pemain. Indeks dari larik ini adalah dari satu hingga enam. Indeks larik terkecil berada di sebelah kiri ditinjau dari sudut pandang pemain.

2. ArrayL adalah larik yang berisi jumlah batu yang terdapat pada lubang di sisi lawan. Indeks dari larik ini adalah dari satu hingga enam. Indeks larik terkecil berada di sebelah kiri ditinjau dari sudut pandang pemain.

3. nLawan adalah variabel yang berisi jumlah batu pada mangkuk lawan.

4. nPemain adalah variabel yang berisi jumlah batu pada mangkuk pemain.

- Penerapan algoritma Greedy

Untuk menggunakan pendekatan greedy untuk menyelesaikan permainan Bantumi, prioritas solusi terbaik harus ditentukan terlebih dahulu. Penentuan prioritas tersebut dapat dilakukan dengan menganalisa peraturan permainan. Berikut adalah asumsi yang digunakan dalam penentuan prioritas solusi yang terbaik hingga yang kurang baik:

1. Prioritas pertama : memilih lubang yang dapat memberikan giliran.

Lubang terpilih adalah lubang dengan jumlah batu yang bila dijalankan, lubang terakhir yang menerima batu adalah mangkuk (berarti mendapatkan giliran). Jika terdapat dua lubang yang

memenuhi prioritas pertama, maka lubang yang pertama kali dipilih adalah lubang yang paling kanan. Pertimbangan ini cukup logis, karena jika lubang yang dipilih adalah lubang yang paling kiri, hal tersebut dapat merubah kondisi lubang di sebelah kanannya. Sedangkan jika lubang yang dipilih adalah lubang solusi yang paling kanan, maka lubang solusi yang lebih kiri tidak akan terpengaruh, sehingga keduanya dapat dijalankan.

2. Prioritas kedua : memilih lubang yang dapat berhenti pada lubang kosong di sisi pemain (mencuri batu lawan yang terbanyak), atau menyelamatkan sebanyak-banyaknya batu sendiri (jika lawan dapat berhenti pada lubang kosong di sisi lawan)

Jika terdapat dua buah pilihan untuk menyelamatkan atau mencuri, maka untuk menentukan pilihan, terlebih dahulu dilakukan perbandingan antara jumlah keuntungan yang akan didapat atau jumlah kerugian. batu yang dapat dicuri lawan. Jika jumlah kerugian lebih kecil dibandingkan jumlah keuntungan. Maka jalankan lubang yang memberi keuntungan. Dan sebaliknya. Apabila terdapat dua atau lebih lubang yang memberikan keuntungan atau kerugian yang sama, maka lubang yang dijalankan adalah lubang solusi yang terletak paling kanan. Hal ini cukup logis pada kasus apabila lawan dapat mencuri batu pemain. Bila lubang yang dijalankan adalah lubang yang lebih kiri, maka dapat menambah jumlah batu pada lubang yang sebelah kanan. Sehingga kerugian bertambah. Jika terdapat lubang yang bila dijalankan berhenti pada lubang kosong, namun lubang lawan tidak terisi batu, dan jika lawan dapat berhenti pada lubang kosong, namun lubang pemain pada arah sejajar juga kosong, maka lanjut ke prioritas ketiga.

3. Prioritas ketiga:

Bila tidak terdapat pilihan lubang yang memberikan solusi prioritas pertama dan kedua. Maka jalankan lubang yang berisi batu, yang paling kanan. Secara logika, lubang tersebut lebih dapat menjangkau mangkuk dan menambah poin. Penerapan algoritma Greedy pada kasus ini adalah dengan memilih pilihan terbaik berdasarkan prioritas pada setiap giliran Himpunan kandidat C adalah semua lubang pada sisi pemain yang ada batunya. (arrayP[i] _ 0, untuk i =1..6). dan himpunan solusi, S adalah salah satu dari himpunan kandidat (arrayP[i] yang dapat memberikan solusi maksimal).

Pseudocode dari penerapan algoritma greedy untuk mencari solusi Bantumi:

function greedyBantumi (input arrayP[1..6]: array of integer)--> indeks

Deklarasi

untung, rugi: integer

indeks : integer

Algoritma

if (cekPrio1(arrayP)= true)

then

indeks <-- cariIndeksPrio1(arrayP)

else

if (cek_Prio2(arrayP = true))

then